Exponent Fractals in Mathematica

This is the mathematica code for a recursive program that generates fractal images representative the powers of some number, p.  For example, p^n=f[p,1,size,0,0,n], where size is a positive number less than 1.  The smaller p is, the more quickly the triangles shrink.

f[p_, size_, ratio_, x_, y_, 0] := Point[{x, y}]
f[p_, size_, ratio_, x_, y_, n_] :=
Table[f[p, ratio*size, ratio, x + size*Sin[2 i*Pi/p],
y + size*Cos[2 i*Pi/p], n – 1], {i, 1, p}]

Here are few coded examples:

Graphics[f[3, 1, .5, 0, 0, 7], ImageSize -> 750]

GraphicsRow[
Table[Graphics[f[3, 1, .5, 0, 0, k], ImageSize -> 300], {k, 4, 6}]]

GraphicsRow[
Table[Graphics[f[4, 1, .4, 0, 0, k], ImageSize -> 300], {k, 3, 5}]]

GraphicsRow[
Table[Graphics[f[5, 1, .35, 0, 0, k], ImageSize -> 300], {k, 3, 5}]]

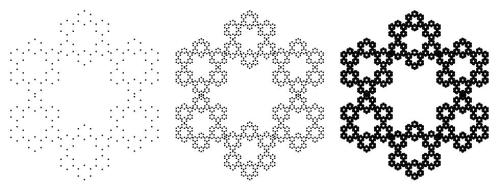
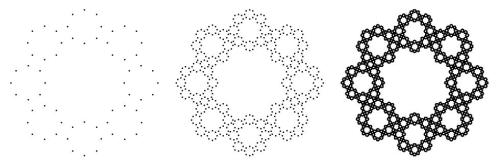
A few uncoded examples:

You might have to play around with the value of ‘size’ for different p values, but you could also try setting size = Sin[Pi/p].