Stars of the Mind’s Sky is the title of a series of works exploring the space of regular star polygons. A star is constructed using two numbers, p and q. By placing p points evenly spaced along a circle and drawing all diagonals that move q spaces over, a star is made.
STAR SPACE
“Star Space” is a 16 by 24 section from an infinite array, including all possible stars. The rows determine the number of points, and the columns determine “jump number” used in generating them. The nth row repeats with period n, and beautiful patterns emerge from the polyrhythms of these repetitions.
Star RingS
 |
 |
 |
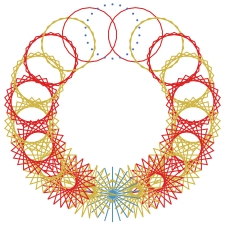 |
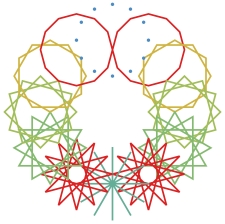
Clockwise from top-left: Seven, Twelve, Twenty-Two, and Twenty-Four
An infinite series of images formed in a simple way: as a ring of n, n-pointed stars arranged along a circle by q, the jump number used in generating them. The stars are colored along a gradient to indicate the number of pieces they come in, with red for single-piece stars. The color patterns illustrate the algebraic properties of the associated cyclic group.
300 Stars in Orbit
Here we see star rings one through twenty-four, arranged concentrically. Algebraically, these represent the subgroups and cosets generated by elements of a cyclic group. They have been colored on a gradient to indicate the number of cosets; a red star signifies a generating element. As a consequence of these structural choices, we may observe congruent stars with increasingly many cosets, shifting their way to blue along central rays through any red star.
Star Sequence

I laser cut a set of twelve-pointed stars from plexiglass and created a few photographs. Star Sequence shows the progression of stars and their inner dodecagons, as the density, q, increases.
Star Stack
 When the six different twelve-pointed stars are stacked, the removed central dodecagons form a sort of bowl. Shot from above, they resemble a K12 graph – the complete graph of possible edges between twelve points.
When the six different twelve-pointed stars are stacked, the removed central dodecagons form a sort of bowl. Shot from above, they resemble a K12 graph – the complete graph of possible edges between twelve points.
 Though the edges of the star stack rise vertically (because all stars are the same size), the stack appears pointy when shot from the other side due to foreshortening. This view gives some sense of the structure’s outside edge.
Though the edges of the star stack rise vertically (because all stars are the same size), the stack appears pointy when shot from the other side due to foreshortening. This view gives some sense of the structure’s outside edge.


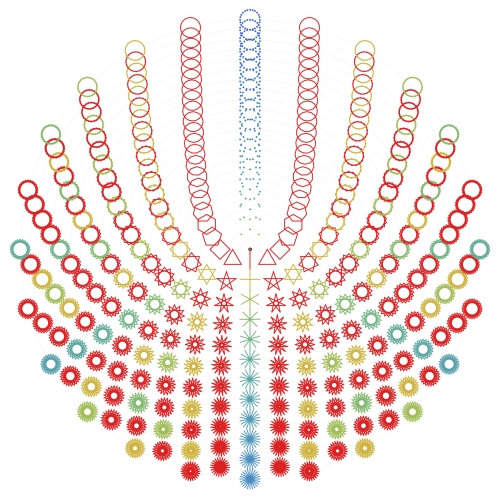

I love the star rings!
Hey thanks, Dan! If you write some good imbalance problems (see my new post) you could win a free print. :)
Paul, what software did you use to make the diagrams? SO BEAUTIFUL!
Thank you so much, Maria! I wrote the code in Mathematica.