Imbalance Abundance

I’m really happy to see how many people have been excited by these imbalance problems.  The entries continue to roll in for my imbalance problem writing contest.  You can check them all out here, and I’ll continue to update that page.  I’m so happy to see other people’s ideas stretch my thinking and help me see what’s possible.  This is just really fun.  I have some early favorites, but I won’t give anything away just yet.  Hopefully I’ll get more submissions.  maybe YOU will make one.

I’m noticing all sorts of techniques for solving them.  In fact, I learned something from a recent submission and it inspired three new puzzles of my own!  I hope you enjoy.  I’d love your feedback.

More Imbalance Problems

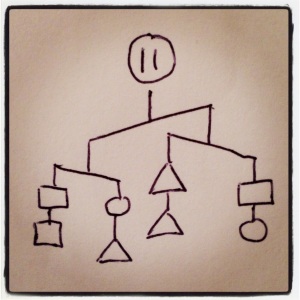
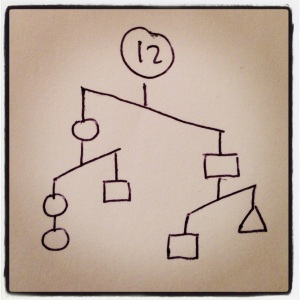
I’m really digging these imbalance problems I came up with.  Friday was our last day before spring break, and I worked on them with every one of my classes.  They liked the puzzles, but the examples I had were a bit too easy, so our real goal was creating good imbalance problems of our own, which is way harder than solving them.  My 5th graders had the best ideas for tweaking the puzzles and making new ones.  It was cool for them to realize you couldn’t just draw a picture, because sometimes they were impossible, and other times they didn’t give enough information.  I’ll hopefully post some of their puzzles after break.

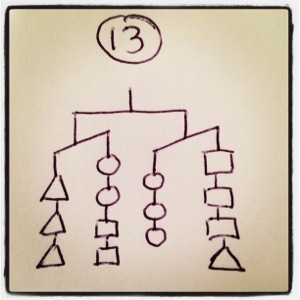
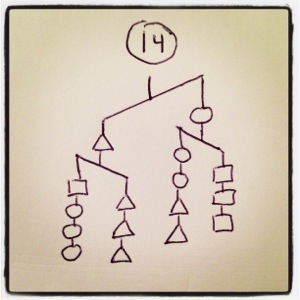
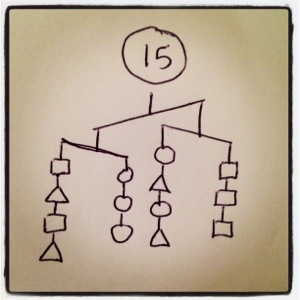
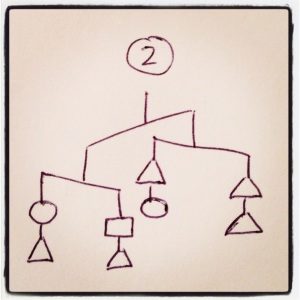
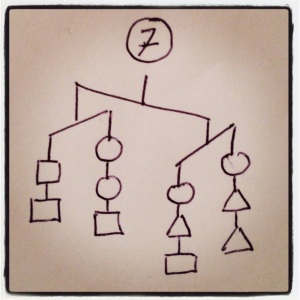
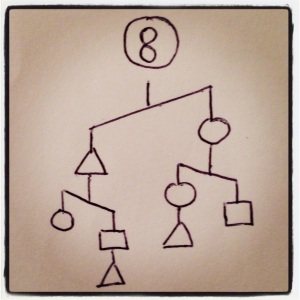
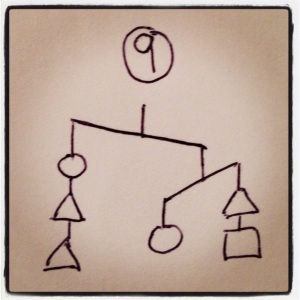
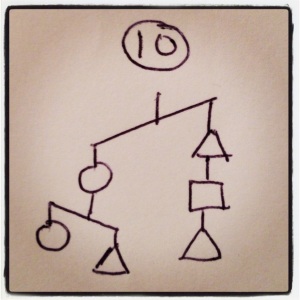
I’ve been working the last two days on my own puzzles, and I’ve never had a better time working with inequalities in my life.  They have a way of sneaky way of revealing information that I’m really liking.  2x<y+z tells you some interesting stuff, for example.  Further down I’ll talk about how I write them, what makes for a good puzzles, and the puzzle-writing contest I’m having, but right now, why don’t you try some out?  I’m especially proud of 6, 9, 10, 11, and 12.  ENJOY!

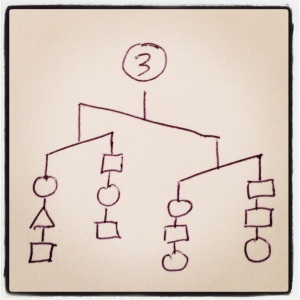
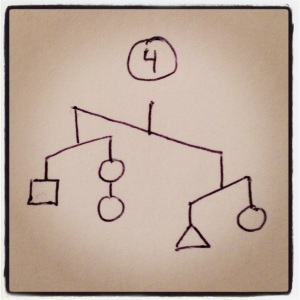
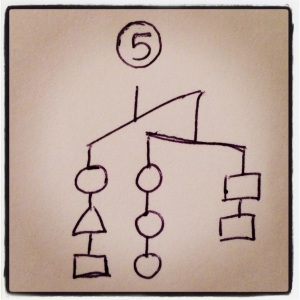
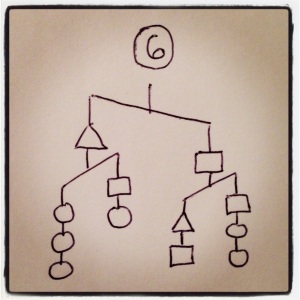
In each case, order the three shapes by weight

Fun, right?  As I’ve said, I’m offering a prize for great imbalance puzzle-writing.  My favorite two puzzlists will receive a print of their choosing from the Stars of the Mind’s Sky series, up to 12″x12″.  Just post your problem(s) in the comments or email lostinrecursion@gmail.com.

So what makes a good puzzle?  It’s a matter of taste (like a lot of mathematics actually), but I tend to like my puzzles pretty simple.  A big, messy, just plain hard puzzle is just a hassle, but something compact and tricky to untangle, now that’s what I like.  I love when a puzzle requires me to think in a new way or exploit some clever little detail I hadn’t considered.  Nathan Chow sent me a really clever puzzle design that implements “entangled imbalances,” which I completely love.  Doesn’t it inspire you to write your own?  I could have cropped it so it didn’t look like an iPhone app, but I love art that reveals the creative process.

In case you’re wanting tips for writing these puzzles, I’ll tell you about my process.  I usually start with a single idea or part of the picture.  The key is thinking about what information it gives the solver, and what other information they’ll need to finish the problem.  After that it’s just a matter of cleverly revealing that information and piecing them together.  Maybe solving the problems above in order will give you a sense of the new ideas I had and was able to wrinkle in.

I hope you’re loving these as much as I am, and I’m dying to see your creations.  Mostly because I want some to solve!!!

Imbalance Problems

(Click here for full page of imbalance problems.)

My fifth graders have been writing problems this week.  Mostly things liks “5 branches have 40 leaves, and 10 trees have 200 branches.  How many leaves will 320 trees have?”  Some of them have been writing problems with symbols that amount to systems of linear equations, and earlier this year we worked on balance problems to get at that sort of thing.

While all this was going on, inspiration struck.*  What if the scales don’t balance?  What if one side weighs more?  Behold, my “imbalance problems.”

Unfortunately, problem 2 cannot be uniquely deduced.  It has two possible solutions.

These are just three I came up with for example, but I can see a whole world of possibilities.  I love how designing them is maybe a better problem than solving them.  How many pieces of information do I need to give (albeit, implicitly)?  [turns out it depends on what the information is! (maybe that’s not surprising.)]

Imbalance Problem Contest

Inspired by this post by the incomparable Shawn Cornally, I’ve decided to offer a little puzzle-writing competition.  Spend some time writing great imbalance problems (the kind that push the state of the art), then share a link to them in the comments.  My two favorite puzzle-writers (based on indescribably subjective criteria) will win a print of their choosing from my Stars of the Mind’s Sky series, up to 12″x12″.  All of the rest of us will get a collection of excellent imbalance problems to solve and share with others!  Exciting right?  Who’s in?

(Click here for contest results)

+ + +

*not a ground-breaking, revolutionary, or truly novel inspiration, I admit.  For me, this is a clear cut Cohen-Ventorism.**  It’s such a slight tweak on an extremely common problem type.  Someone else (countless others) must surely have also come up with this.  And yet, a google search for “imbalance problems” yielded surprisingly little.

** Cohen and Ventor are two imaginary mathematicians who completely independently, perhaps simultaneously, discover (or coinvent) all sorts of mathematics.  (See Newton and Leibniz)